Bomb Threats, Global Warming and Decision Making: An Educational Experience
Global warming is one of the world’s most argued topics. The majority of people agree that the global warming is real, but the most controversial aspect is whether it is caused by humans or simply part of a cyclical process of nature. This paper presents an argument that regardless of the cause of global warming, there is only one logical response for society to make. The argument can aid students understanding of the tension between public policy and rigorous scientific inquiry when decisions could lead to environmental and human harm.
1. INTRODUCTION
Global warming is the most pressing environmental issue society faces (IPCC, 2007). According to Stern’s summary of conclusion (2006, pg. 1) inaction can lead to “risks of major disruption to economic and social activity, on a scale similar to those associated with the great wars and the economic depression of the first half of the 20th century.” The consequences of not acting are severe and damages might be irreversible.
In this paper we consider global warming as an example to instigate classroom dialogue in order to understand the consequences of decision making when errors are made.[1] Exposing students to global warming problem in a statistics course reveals to them the tension, or a trade-off, between public policy decisions to avoid environmental and human harm, and that of scientific rigorousness required by conventional statistical methodology.[2]
The issue as to whether or not global warming is caused by anthropogenic forces can stimulate students’ interest and understanding of the philosophy underlying scientific inquiry. Asking students “what do they think” when someone claims that humans are the cause of global warming from a statistical perspective promotes strong classroom discourse.[3] Students can ponder the setup of the null (considered true) and alternative hypothesis. They can decide to take as truth that humans are the cause of global warming due to principle 15 of the 1992 Summit on the Environment and Development, known as the precautionary principle.[4] Other students might follow article 11 of the Universal Declaration of Human Rights (UDHR). Article 11 of UDHR states: “Everyone charged with a penal offence has the right to be presumed innocent until proved guilty according to law in a public trial at which they have had all the guarantees necessary for their defence.”[5]
The precautionary principle can be interpreted as a shift of the burden of proof to humans and comes into conflict with article 11 of the universal declaration of human rights. Furthermore, students can discuss the type I and type II errors, the costs of these errors, and the consequences of their decision to accept or reject the null hypothesis.
In the remainder of this paper, the following sections are presented. Section 2 presents the examination question on global warming posed to our students in 2007 and which has led to this paper. This is followed by an introduction to hypothesis testing, an analogy with the justice system, and the setup of the global warming hypothesis. Section 4 discusses bomb threats and their association with global warming. The cost and consequences of our decision are discussed in section 5. Finally, in section 6 we offer some concluding remarks.
2. THE PROBLEM
In February of 2007, the following mid-term exam question was posed to students attending a second-year course in Statistics for Business and Economics at Thompson Rivers University. This course was the second part of a full-year course in statistics and the question was posed to refresh their memories on what hypothesis testing was about.
A claim is made that global warming is caused by humans. Set up the null and alternative hypothesis for this claim. As a scientist, you want to test that the above claim is true beyond a reasonable doubt. Describe the type I and type II errors in terms of the above problem. Also discuss the implications of the errors in terms of their associated costs.[6]
While drafting the answer to the exam question, it was realized that this question had very strong implications as to whether or not immediate action is required to contain global warming.[7
3. HYPOTHESIS TESTING, CRIMINAL JUSTICE AND GLOBAL WARMING
Hypothesis testing is used in scientific inquiry to determine whether a value assigned to an unknown population parameter is valid or not. There are two hypotheses: the null hypothesis (Ho) and the alternate hypothesis (Ha).[8] The null hypothesis is considered true until significant evidence is found to conclude otherwise. If that occurs, the null hypothesis is rejected and the alternate is proven to be true. If not, then there is insufficient evidence for the alternate hypothesis to be proved.
For either decision, there is a possibility of making a correct decision or making an error. Given two decisions (i.e., reject or accept Ho) and two states of nature (i.e., Ho is true or false) there are four possible outcomes.[9] Each outcome has an associated probability attached. First, rejecting Ho when Ho is true is a type I error. The probability is known as the level of significance, and is denoted by α. In a typical scientific study this probability is set at very low levels. For example, a 5 percent level is often chosen. The selection of a low value for α is due to the fact that the null is given the benefit of the doubt. There is a 5 in 100 chance of rejecting Ho when Ho is true if α = .05. Thus if the scientist is concerned that a type I error is going to have serious costs a lower level of significance is chosen. As long as the evidence is strong enough, the scientist will reject Ho and most probably make the right decision. Rejecting Ho based on the sample evidence does not imply certainty in decision making as there is still a small probability of making a type I error. Second, accepting Ho when Ho is true is the correct decision and the probability of this happening is given by the level of confidence level, 1-α. When conducting a scientific inquiry the confidence level is usually set very high because the null hypothesis is given the benefit of the doubt. The third outcome is the decision to accept Ho when Ho is false. This is known as a type II error and its probability is denoted by β. This later probability depends, amongst other variables, on the sample size, the level of significance, and the true value of the population parameter relative to the hypothesized value under Ho. Finally, the decision to reject Ho when Ho is false is the correct decision. The probability of this happening is measured as (1-β) and is known as the power of the test. The table below summarizes the four cases.
Table 1: Decisions and Statistical Errors
| State of Nature | |||
| Ho is True | Ho is False | ||
| Decision | Reject Ho | Type I error
α |
Correct Decision
(1-β) |
| Accept Ho | Correct Decision
(1-α) |
Type II errorβ | |
A very good analogy of hypothesis testing is the operation of the justice system in modern democracies (Feinburg, 1971). A person caught in a crime is presumed innocent (the null hypothesis). The accused is given the benefit of the doubt. The two hypotheses in a court case can be stated more formally as:
Ho: The defendant is innocent
Ha: The defendant is guilty
The presumption of innocence gives the accused the right to defend the accusations. It is based on the assumption that most humans are not expected to be criminals. To be convicted of a crime, the person’s guilt has to be proven “beyond a reasonable doubt.” The evidence brought to the case must indicate beyond a reasonable doubt that the person is guilty (the alternative hypothesis). A juror knows that deciding to convict a person of a crime, because the evidence indicates guilt beyond a reasonable doubt, does not imply certainty. A “shadow” of doubt always exists.[10]
In the criminal justice example, the Type I error would be to convict an innocent person, while the correct decision would be not to convict an innocent person. On the other side, a Type II error would be to set a criminal free, while the correct decision would be to convict a criminal.
In the global warming question, the appropriate hypotheses are:
Ho: Humans are not the cause of global warming
Ha: Humans are the cause of global warming
In considering the errors under the global warming hypothesis, the Type I error would be to conclude that humans are the cause of global warming when in reality they are not, while the Type II error would be that we cannot prove that humans are the cause when they actually are. Again, both errors have repercussions, so what level of significance should be chosen?
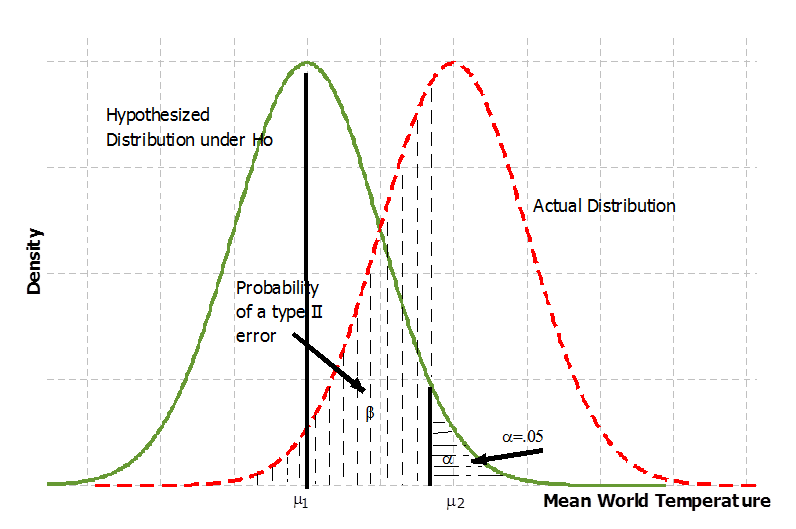
The probability of a type I error is shown as the gray area in Figure 1 when the level of significance is say 5 percent.
The climate attribute, global mean temperature, follows a normal distribution bell shaped curve (e.g., say a global population mean µ = 14 Celsius).[11] When Ho is true the hypothesized distribution under Ho and the actual distribution from which the sample is drawn are the same. When Ho is true, most of the time the sample evidence will be drawn from the area that is around the population mean µ. Hence, a scientist will accept Ho when in fact Ho is true making the correct decision.
The sample evidence in recent years has world temperatures appearing to the right of the above distribution. According to Hansen et al. (2006) global surface temperature has increased by approximately 0.2 Celsius per decade in the past 30 years. The instrumental record of climate shows an approximately .7 ± 0.2 Celsius warming over the last century (IPCC 2007). Is the increase in world average temperature caused by human activity or is it a random drawing event? A researcher equipped with strong evidence against the null might decide to reject Ho believing that Ho is false. The scientist might conclude that humans are the cause of global warming when in fact they are not. The sample evidence could be due to a random drawing not representative of the population. This is known as a sampling error. For example, Svensmark (1998) argued that the recent warming is caused by the level of cosmic rays hitting the earth. However, most scientists associate the recent warming with human activity in terms of burning fossil fuel and land use change.[12] The scientist role is to try and account for the most important factors and to examine their influence on the pattern of the average world temperature.
Scientific research assigns a low chance (probability) of the type I error occurring in the same way that jurors want to minimize the chances of convicting an innocent person. The probability of a type I error is usually chosen by the researcher and its value depends on the cost of such an error. Furthermore, the smaller the probability of a type I error the more difficult it is to reject Ho on the basis of the same information.
The probability of a type II error is shown in Figure 2 below and is usually denoted as β.
When Ho is false the hypothesized distribution under Ho is different from the actual distribution. The random sample is drawn from the actual population. Figure 2 shows the actual distribution to the right of the hypothesized distribution. This indicates a permanent increase in the population global mean temperature from µ1 to µ2. Most observations, from the sample drawings, will fall into the rejection region as these sample results would appear, more frequently, around the new global mean population value (e.g., say new world population mean of µ1 = 20 Celsius). Scientists would be rejecting Ho when in fact Ho is false and making the right decision. The further to the right the actual distribution is the stronger is the power of the test to reject a false hypothesis. The probability of a type II error, β, is obtained for values that fall in the non-rejection region to the left of the area α and bounded by the area of the actual distribution. The power of the test denoted as 1-β to detect a false null is indicated by the area to the right of the actual distribution above the critical value determined by the choice of α. In the diagram β is represented by the vertical dashed lines, while the probability of a type I error, α, is represented as before by the horizontal dashed lines under the hypothesized distribution. What is important to note is that the probability of making a type II error is usually larger than that of a type I error with conventional statistical methodology. In the analogy of the justice system the institutional framework of modern democracies is designed to minimize the chances of convicting an innocent person. The hypothesis of innocence is only rejected when the error of convicting an innocent person is very unlikely. Similarly, in statistics the error is controlled by the researcher to be as small as possible. As a consequence of this asymmetric behaviour, the type II error (setting free a guilty person), is often comparably large. Presumably society places a higher cost to convicting an innocent person relative to the cost of setting free a criminal.[13]
There are certain well known properties about the behaviour of the probability of a type II error, β. First, the probability of a type II error, β, is larger the closer the new population mean is to the hypothesized value for a given α. For example, if the new population mean global temperature is 1 Celsius higher relative to the hypothesized level, the probability of a type II error, β, will be larger than if the new population mean global temperature is 5 Celsius higher from the hypothesized level, ceteris paribus. Second, the two probabilities α, β vary in opposite directions. If a scientist decided to reduce (minimize) the probability of making a type I error, α, it will increase (maximize) the probability of making a type II error, all else the same. In the analogy of the justice system, if we reduce the probability of convicting an innocent person we are increasing the chances of letting free a criminal. In the global warming case, as we reduce the probability of concluding that humans are the cause when in fact it is a random event, we are increasing the probability of letting humans continue the current path. When one deals with environmental issues the probability of a type II error seems much more serious than the probability of making a type I error. Should the scientist then minimize the probability of a type II error instead of minimizing the probability of a type I error when it comes to environmental issues? This is not the convention of the established methodology of statistical research. Which strategy is better to follow depends on the relative costs of these errors as we discuss in section 5.
To further understand this, we can examine another example which has little argument.
4. BOMB THREATS AND THEIR ASSOCIATION WITH GLOBAL WARMING
In 2000, a bomb threat was phoned in to Thompson Rivers University. Fortunately, no bomb was found. This event led to an interesting discussion in an introductory statistics class the next day:
You are the president of the university and you have to make a decision when the bomb threat is phoned in using the following hypotheses:
Ho: There is no bomb
HA: There is a bomb
Following the conventional statistical testing procedure, the null is set up so that innocence is considered true. The students are asked what level of significance they would use to make this decision. This would depend on the cost of a type I error versus the cost of a type II error. A type I error is to conclude that there is a bomb when in fact the bomb scare is a sham, while a type II error is one where you are unable to prove that there is a bomb when there is one.
After a fair amount of discussion, the students typically decide to set the level of significance at 1. In other words, they would always reject the particular null hypothesis and conclude that there was a bomb. That is the precise call the university administration made. They decided to close down the university for that day.
The consequences and costs of making a type II error were too severe. Students figure that the cost of a type I error is negligible. Temporary disruption of service and evacuation of the university, the cost of checking for suspicious objects, and closing down the university for that particular day to avoid any possible human tragedy are some of the costs considered by students. When discussing the type II error, students realize that there can be loss of human lives.[14] They are not willing to take that chance. Thus, the students decide to support the precautionary principle by minimizing a type II error instead of minimizing a type I error.
The analogy to the bomb threat is even more interesting when we consider the actions taken. A bomb threat is called in, and almost invariably the decision is to reject the null hypothesis of “there is no bomb” and conclude there is. And everyone agrees with the decision. No one wants to see avoidable loss of human life. In reality, those making the decision do not believe that there is a bomb. They just refuse to commit to making a Type II error.
Some scientists consider global warming induced by anthropogenic forces, from the burning of fossil fuel and land use changes, as a threat to our existence and hence a major bomb which might occur in the distant future (Lovelock, 2010); a ticking bomb which if left unchecked can explode and destroy civilization.
Now, when students were asked to set the level of significance in this case, we’d typically have values varying from 0 to 1. The 0s would be adamant that humans causing global warming was completely false, while the 1s would be just as sure that it was true. But many would likely pick values in the middle somewhere. So how do we make the decision?
To decide on a level of significance, we need to clearly understand the consequences of the Type I and II errors in this example.
5. THE COST OF OUR INCORRECT DECISIONS
Let’s look at the costs of each incorrect decision:
Considering the possible errors, a Type I error means it was concluded that global warming is caused by humans, but it actually isn’t.[15] In that case, governments will provide incentives in order to urge the population to change their activities. This could include conserving energy, recycling, and developing alternative energy sources (wind, solar, hybrid). Of course, there will be some monetary costs in doing this, but those will likely be incurred in any event, and there will also be substantial cost-savings and business opportunities from the new technologies (Porter, 1991, Stern, 2007). Given that we have a finite amount of conventional energy available, these would be appropriate activities to undertake regardless of the cause of global warming. Even if it is not human-caused, these steps will likely have to be taken in the future in any event; the concern of global warming simply accelerated the time frame. So the actual consequences of taking this action are not negative, even if global warming is not caused by humans. The cost of a type I error is to switch production from the current high-carbon-intensive sectors to new low- carbon-intensive sectors (an opportunity cost in economists’ terminology), adjustment costs and possibly some temporary adaptation costs. Stern (2007) estimates the costs to stabilize greenhouse gas concentrations at 550 ppm is approximately 1 percent of global GNP per year with a range from -3.9 (net gains due to energy savings from green investments) to 3.4 percent of GNP.[16]
Now consider the Type II error, where we fail to act on global warming, even though it is human caused. Accepting Ho when Ho is false implies that our actions, as stated above under the acceptance of Ho, will not be sufficient to deal with the problem and will lead to additional costly mistakes.[17] The consequences could be significant. The cost of a type II error is associated with doing business as usual (BAU), and staying the course where humans continue to change the earth’s climate. The cost of a type II error is the economic impact or the damage brought about by human induced climate change which will appear in the future and also the adaptation costs. These costs could be as high as humankind destroying itself if the human activity increases global average temperature beyond 5 Celsius.[18] The 5 Celsius and beyond range is considered the difference between the temperature during the last ice age and today’s temperature (Lovelock, 2010). Rising sea levels and temperature, as well as increased climate variability caused by human lifestyles, will have an impact on health, agriculture, forestry, water, coastal areas, as well as on many different species and the ecosystem. The cost of making this error is the cost associated with impacting all of the above mentioned areas. Some or all of that cost could have been lessened by taking action. Stern (2007) stated that inaction could have a very high cost. Stern’s conservative estimate is 15 percent of global GDP by 2200 under the high climate scenario.
One of our statistics students said when answering the question:
“The cost of a type I error would mean spending a great amount of money and time focussing on how we can stop humans from causing global warming when humans are not the problem, but the cost of a type II error would mean spending a great deal of money and time on finding what is causing global warming and then continue to work on some factor of global warming, but not focussing on the real factor, humans.”
6. CONCLUDING REMARKS
When there is a bomb scare, we regularly take a precautionary approach to avoid a type II error. In the global warming case, we have yet to see a strong precautionary approach to the problem. This might be due to ambiguity aversion today and in the future. Humans show averse behaviour when dealing with ambiguity in the near future (e.g., a sudden bomb threat), but less averse behaviour when ambiguity is in the distant future (Onculur, 2010).
Exposing students to the above global warming problem not only makes statistics interesting to students, but also reveals to them a tension or a trade-off between policy decisions to avoid environmental and human harm, and that of scientific rigorousness which requires the minimization of a type I error (Lemons, Frechette and Cranor, 1997). Students can learn that there are a number of reasons why scientists attempt to minimize a type I error when conducting a scientific inquiry, but this sometimes is not appropriate from a policy perspective. Minimizing a type I error makes science rigorous and reduces speculative knowledge. It is also transparent in that the probability of a type I error is documented. Further, it provides a benchmark with which other scientific studies can be compared. Finally, it protects the status quo.
However, students often question the protection of the status quo if it results in environmental or human harm. On what moral grounds should the status quo be protected and give it the benefit of the doubt? Should there not be a moral preference to increase, not minimize, the chances of making a type I error when dealing with environmental harm issues? It might be the case that students prefer to take the precautionary approach and minimize a Type II error in order to protect all species and the ecosystem.
Students could keep the conventional methodology, but be taught to consider making the significance level more liberal when dealing with environmental harm. By selecting a significance level that is on the liberal side, say α=.20, in the conventional statistical methodology, they implicitly attempt to strike a balance between the scientific approach and the policy decisions on such important issues. This balancing act should depend on the estimation of the economic and other costs associated with either of the two types of errors.
In the global warming case, the probability of making a type II error can be considered to be high because of lags in the climate system to translate increased current CO2e concentration in the atmosphere to world mean temperature increases (IPCC, 2007). Thus, if global warming is true, the power of the test (the probability of rejecting Ho when Ho is false) will be stronger in the future as the world mean temperature will be further way from the current hypothesized value of no change. The world average temperature has warmed by .7 Celsius over the last century and is expected to increase further even if C02e emissions are completely eliminated today. This means that the power of the test could be stronger in the future relative to today.[19] But is it correct for public policy makers to wait until the power of the test is strong enough to take action?
The consequences of a Type II error are so serious that they must be avoided even if the costs of government intervention are significant. The consequences of a Type I error are that we will take the same steps that we would have had to at a later date, and those consequences actually have some positive aspects. Much like the bomb example, the logical course of action is to set our level of significance at 1 and always conclude that global warming is caused by humans. Even if we are incorrect, the earth will be better off for it.
REFERENCES
Bellavancea, François, Georges Dionneb, and Martin Lebeau, “The value of a statistical life: A meta-analysis with a mixed effects regression model,” Journal of Health Economics, 28(2), 2009, 444-464
Feinburg, William E., Teaching the Type I and Type II Errors: The Judicial Process, The American Statistician, Vol. 25, No. 3 (Jun., 1971), pp. 30-32
Garfield, Joan, and Michelle, Everson, (2009), “Preparing Teachers of Statistics: A Graduate Course for Future Teachers,” Journal of Statistics Education, 17(2), 2009.
Hansen, James, Makiko Sato , Reto Ruedy, Ken Lo, David W. Lea, and Martin Medina-Elizade. “Global Temperature Change.” Proceedings of the National Academy of Sciences, 103, 2006, 14288-14293.
Holland, Bart, K., “A Classroom Demonstration of Hypothesis Testing,” Teaching Statistics, 29(3), 2007, 71-73.
Intergovernmental Panel on Climate Change, (2007), Climate Change 2007: Synthesis Report. Summary for Policymakers.
Lemons, Shrader-Frechette and Cranor, “The Precautionary Principle: Scientific Uncertainty and Type I and Type II Errors,” Foundations of Science, 2(2), 1997, 207-236
Lovelock, James, “The Vanishing Face of Gaia: A Final Warning” 2010, Penguin Books.
Minard, Anne. “Global Warming Inaction More Costly Than Solutions?” National Geographic News, (2007, September 24). Retrieved on November 8 2010 from
http://news.nationalgeographic.com/news/2007/09/070924-global-warming.html
Neyman, J., and E.S. Pearson, (1933), On the Problem of the Most Efficient Tests of Statistical Hypotheses. Phil. Trans. R. Soc., Series A, 231, 289–337.
Onculer, Ayse, “How do we manage our future? Ambiguity Today is not Ambiguity Tomorrow” in The Irrational Economist by Erwann Michel-Kerman and Paul Slovic, Public Affairs New York, 2010, 107-115
Oreskes, Naomi., “The Scientific Consensus on Climate Change,” Science, 306, 2004, 1686
Porter, Michael, “America’s Green Strategy,” Scientific America, 264(4), 1991, 96.
Stern, Nicholas, “The Stern Review on the Economics of Climate Change: Summary and Conclusion.” 2006, http://www.hm-treasury.gov.uk/sternreview_index.htm
Stern Nicholas, “The Economics of Climate Change: The Stern Review, January 2007, Cambridge University Press
Svensmark, Henrik, “Influence of cosmic rays on Earth’s climate,” Physics Review Letters, 81, 1998, 5027-5030.
Thompson Rivers University, “Statistical Analysis Debunks Climate Change Naysayers.” ScienceDaily. (2007, March 19). Retrieved on November 8, 2010, from http://www.sciencedaily.com /releases/2007/03/070319110332.htm
Weitzman, Martin, “On Modeling and Interpreting the Economics of Catastrophic Climate Change.” The Review of Economics and Statistics, 91(1), 2009, 1-19
Whitman, Q. James, 2008, The Origins of Reasonable Doubt: Theological Roots of the Criminal Trial, Yale University Press, New Haven and London.
[1] The benefits of using classroom discourse in a statistics course are illustrated in Garfield and Everson (2009).
[2] The main idea of this paper has relevance not only in statistics courses but also in many other courses that deal with issues of sustainability. For these other courses, the instructor can omit the technical part of the paper and focus on the public policy aspects of the paper.
[3] Many students taking an introductory course in statistics have a difficult time understanding hypothesis testing (Holland, 2007).
[4] Principle 15 states: “in order to protect the environment, the precautionary approach shall be widely applied by States according to their capability. Where there are threats of serious or irreversible damage, lack of full scientific certainty shall not be used as a reason for postponing cost-effective measures to prevent environmental degradation.”
[5] United Nations General Assembly, December 10, 1948, Paris
[6] Since 2007 the term commonly used is “climate change” instead of “global warming”. We will continue to use the term “global warming” as anthropogenic activities (i.e., burning of fossil fuel and land use changes) are expected to increase the global average temperature. However, either term can be used in the problem without affecting the argument and conclusion of the paper.
[7] For the earlier impact of the answer see Minard (2007) and Thompson Rivers University (2007).
[8] Hypothesis testing was originally developed by Neyman and Pearson (1933).
[9] When sufficient proof is not available statisticians usually use the term “fail to reject Ho”. This means the result is inconclusive and further evidence is required to reject Ho.
[10] Whiteman (2008) argues that the term “beyond a reasonable doubt” was originally designed to make to make conviction easier. The term assured jurors that their souls would be safe if they voted to prosecute the accused. According to Whiteman the term “beyond a reasonable doubt” had very little to do with the rule of law or society’s liberal values and more to do with theology.
[11] This is a reasonable assumption due to the central limit theorem. Some climate studies examine temperature anomaly which is defined as the difference between recent global average temperature level relative to some historical average level, say an average from 1961-1990 (Hansen et al (2006), Man and Jones (2003)).
[12] The 2007 Intergovernmental Panel on Climate Change (IPCC) report concluded that global warming was very likely (90%) to have been caused by humans.
[13] Is this also what society places when it comes to humans and global warming? We will explore this question later in the paper.
[14] According to numerous cost-benefit studies, loss avoided is measured in millions of dollars per life saved. The value of a statistical life (VSL) has a wide range starting from as low as $.5 million and rising to $50 million (in 2000 US$) per life saved (Bellavancea, Dionneb and Lebeau, 2009).
[15] On the other hand, rejecting Ho when Ho is false is the correct decision and would require not only measures to adapt to global warming, but more important measures to mitigate (reduce) the effects of global warming. This is the position of most scientists (IPPC, 2007; Oreskes, 2004). Oreskes examined the abstracts of 928 peer-reviewed papers related to global warming. Oreskes found that none of the papers disagreed with the consensus position. This position being that human activity is the primary cause of global warming.
[16] Table 10.1 of the Stern Review
[17] Accepting Ho “Global warming is not caused by humans” when in fact Ho is true is the correct decision.
[18] Weitzman (2009) based on scientific findings indicates that the probability of a catastrophe climate change is non-negligible and argues that the economic consequences of fat-tailed structural uncertainty outweighs the effects of discounting in a cost-benefit study.
[19] In addition, climate variability is expected to increase with global warming IPCC (2007). This makes the power of test even weaker to detect a false null hypothesis as the variance of the actual distribution is larger than the hypothesized.










 Dave Tomkins is a Senior Lecturer of Mathematics and Statistics at Thompson Rivers University in Kamloops, British C olumbia, Canada. His main research interests include gambling theory, probability and risk management. He was recipient of the 2008 Teaching Excellence Award at TRU.
Dave Tomkins is a Senior Lecturer of Mathematics and Statistics at Thompson Rivers University in Kamloops, British C olumbia, Canada. His main research interests include gambling theory, probability and risk management. He was recipient of the 2008 Teaching Excellence Award at TRU.  Peter Tsigaris is an Associate Professor of Economics at Thompson Rivers University in Kamloops, British Columbia, Canada. His research interests span the areas of environmental economics, taxation, decisions under risk, and the education of economics. In 2007, TRU awarded Dr. Tsigaris its Research and Teaching Excellence awards. This is the first time both awards have been won by a single faculty member in the same year.
Peter Tsigaris is an Associate Professor of Economics at Thompson Rivers University in Kamloops, British Columbia, Canada. His research interests span the areas of environmental economics, taxation, decisions under risk, and the education of economics. In 2007, TRU awarded Dr. Tsigaris its Research and Teaching Excellence awards. This is the first time both awards have been won by a single faculty member in the same year. 

Several issues:
1) You point out in a footnote that scientists use the term “failure to reject Ho” when statistical significance is not achieved in the data, but in the main body of text seem to be inferring that this is equivalent to “accepting Ho as true”, which is, at best, a gross misrepresentation. Failure to reject implies that the scientist cannot make any statement concerning the truth/falsity of Ho. It implies that we are still in the dark about the hypothesis, not that we embrace it as a fact. As a result, you are misrepresenting the scientific inference process by saying “scientists accept Ho”. It requires extraordinary circumstances in order for something approaching that sort of decision to occur (i.e. repeated failure to reject with extremely powerful tests).
2)By your logic, we should set P(Type-I) = 1.00 for any and every Ho/H1 combination we might entertain for a particular phenomenon. For example, your arguments in favour of doing so might equally apply to the following:
Ho: unicorn farts are not responsible for global warming
H1: unicorn farts are responsible for global warming.
In what way would we be any less morally accountable if it turns out Ho is actually false? Is this argument sufficient to cause us to relax our rejection standards more in favour of finding H1 to be true?
The example above was not intended to ridicule the thesis put forward in this paper. Rather, I wanted to point out that the paper appears to be confusing the evidence that global warming is occurring with the potential causes for said phenomenon. Failing to reject Ho does not imply there isn’t a cause for global warming. It simply means, in the face of repeated failure to reject, a different hypothesis might be entertained, and altering a relatively useful rule-of-thumb with regard to setting rejection regions in order to put a particular H1 on more equal footing with Ho implicitly rejects all other possibilities out of hand.
Thank you for your feedback. This is precisely the aim of the article to initiate such discussions with students about scientific inquiry.
Regarding the Accept Ho/Fail to Reject Ho comment, we certainly understand that accept Ho can leave the wrong impression in hypothesis testing – hence the footnote. But by failing to reject the null hypothesis in this particular example, we will not take action on global warming. We believe that in this example by not taking action, we are implicitly accepting that global warming is not caused by humans.
As far as the unicorn fart example. We understand the point you are making. If we are going to conclude that unicorn farts cause global warming, what steps would we take? Perhaps kill all the unicorns. We would eliminate a species – serious consequences there. The difference, as was stated in the article, is that in our example the steps we are taking to deal with global warming would eventually need to be taken regardless of the cause of global warming, so why not take them now? In the unicorn example, we could not say that “well, we were already going to kill all the unicorns anyways”…that’s what we believe makes the difference.
Thanks again for your comments.
It appears to me that you’re also dismissing the gravity of a type II error. What if warming isn’t caused by humans and bad consequences will result no matter what we do (or if it is caused by humans but can’t be reversed)? In that case, we’d be better off putting all our effort into preparing for the inevitable and would be wasting valuable time, energy and resources if we focused instead on reducing “anthropogenic forces”.